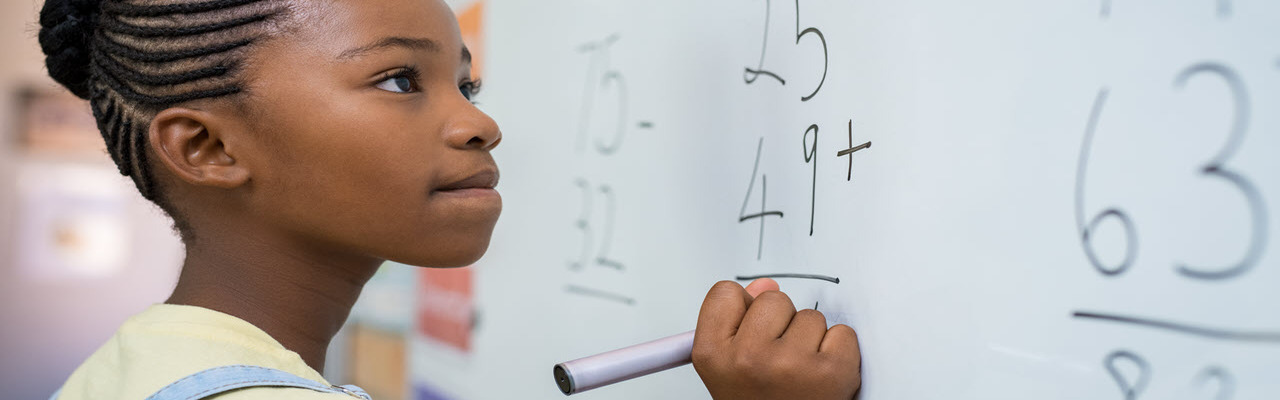
MISE EN CONTEXTE
Usage de l'écran interactif en mathématiques
De belles réussites sont à noter, notamment dans les logiciels destinés aux écrans interactifs et plus particulièrement pour la géométrie dynamique. Citons, par exemple Cabri, qui proposa le premier logiciel de géométrie dynamique et qui s’est depuis diversifié dans tous les domaines des mathématiques, Géométrix, Geoplan/Geospace et TracenPoche de l’association Sésamaths qui édite aussi InstrumemPoche, une trousse d’outils virtuels pour la géométrie.Notons toutefois que cet élan français a été freiné par le développement tardif des solutions interactives dans notre pays. D’autres pays, mieux équipés, on alors pris la relève, avec notamment les éditeurs de logiciels de surfaces interactives, notamment SMART Technologies et Promethean ou des éditeurs comme RM (GB, pays équipé à 100 %) avec easiteach ou Geogebra d’origine autrichienne, mais très largement utilisé dans le Monde, y compris en étant intégré dans certains logiciels d’écrans interactifs.
Retenons de ce petit historique que l’écran interactif est l’outil parfait pour l’utilisation en classe des logiciels de géométrie, d’autant plus qu’il peut être relayé sur les outils des élèves, tablettes et ordinateurs, ce qui permet aux étudiants de reproduire de façon individuelle les démonstrations et constructions réalisées en classe.

Dans le domaine de la numération, là encore, les pays anglo-saxons ont pris les devants, mais la bonne nouvelle est que la majorité des activités dans ce domaine peuvent être abordées avec le logiciel livré avec l’écran interactif. L’approche est généralement ludique, faisant souvent appel à des quizz et d’autres activités stimulantes. L’écran est un bon outil pour déstresser les apprenants en mathématiques. Rappelons à ce sujet, les travaux de Morin (1997) sur la valeur académique d’une tâche scolaire (arts plastiques versus géométrie). Des exercices de reconstitution de figures géométriques en classe de troisième étaient présentés aux élèves comme des exercices d’arts plastiques à la moitié de la population et comme des exercices de mathématiques à l’autre moitié. Cette étude a démontré que dans un contexte à faible enjeu académique, les arts plastiques, les élèves ayant des difficultés en mathématiques réussissaient mieux si l’activité était présentée comme une réalisation d’arts plastiques. L’écran interactif permet largement de jouer de cette ambiguïté, les mathématiques peuvent devenir un jeu.
Pourquoi utiliser l’écran interactif en classe de mathématiques ?
Le compas dans l’œil
Si small est souvent beautiful, big peut l’être aussi. La maladresse de la tenue d’un compas ou d’une règle peut être compensée par les performances des outils destinés aux écrans interactifs. Ces derniers peuvent être intégrés dans les logiciels des écrans interactifs ou utilisés séparément.
Les enseignants qui connaissent la galère de tracer un cercle sur un tableau à craie avec un compas à ventouse usagé, ne peuvent qu’apprécier les outils parfaitement conviviaux des écrans interactifs.
Dis-moi ton nombre
La numération et la construction du nombre sont une des activités les plus essentielles de l’apprentissage en primaire. Cela passe par beaucoup de manipulations. Les écrans interactifs permettent d’effectuer ces manipulations en grande taille, pour permettre de partager la réflexion entre de nombreux élèves. Voir un exemple avec des MS, GS et CP.
Soyons reconnaissants à la reconnaissance
Tracer des lignes bien droites, éventuellement longues et en plus parallèles ou perpendiculaires entre elles est souvent malaisé sur un tableau traditionnel. Avec un écran interactif, rien de plus simple. Avec la reconnaissance de forme intégrée à la plupart des logiciels d’écrans interactifs, il suffit de tracer un trait à main levée puis de le faire reconnaître comme droite. Si l’inclinaison n’est pas bonne, il suffit de réorienter la ligne.
Encore plus facilement, certains logiciels effectuent automatiquement la reconnaissance de forme. Il suffit de tracer une vague ligne droite, un rectangle, un cercle ou un triangle pour les voir se matérialiser de façon parfaite. Cela n’est pas forcément une bonne chose quand ou souhaite expliquer la minutie nécessaire pour les tracés en géométrie, mais cela permet rapidement d’avoir un trait bien droit pour une opération posée en colonne sans devoir prendre une règle à chaque fois.
Le naturel revient au galop
Les mathématiques « naturelles » consistent à repérer dans l’environnement des éléments mathématiques. Il peut s’agir de la frise d’un vêtement, de la reconnaissance d’éléments géométriques dans la nature ou de notions plus complexes, tirées de « la vraie vie ».
L’écran interactif, associé à sa galerie, est un merveilleux instrument pour ces activités. En effet, il est possible de classer des éléments selon différents critères mathématiques et de les exploiter instantanément en cas de besoin. C’est extrêmement précieux dans cette approche des mathématiques où la création d’un répertoire commun est essentielle.
De façon plus basique, cette galerie peut contenir aussi toutes les ressources souhaitées, notamment des tracés millimétrés et des figures géométriques.